近日👎🏼，在理學院葛先輝教授指導下🔲，應用物理學專業兩名本科生柏辰🙍🏼‍♀️🙆、李文浩在量子復雜度研究方面取得重要進展。成果以題為“Toward nonequilibrium thermodynamic analog of complexity and Jarzynski identity”的論文發表在國際著名期刊《Journal of High Energy Physics》上。物理系本科生柏辰和李文浩分別為為論文第一作者和第二作者🚶🏻‍➡️，葛先輝教授為論文通訊作者。

柏辰和李文浩為2018級應用物理專業本科生，2019年進入葛先輝教授課題組，學習AdS/CFT對偶🔇、量子復雜度以及非平衡態物理並參與科研，即將分別前往中國科學院卡弗裏理論科學研究所以及中國科學技術大學攻讀研究生。

量子復雜度是近年來量子論和理論物理研究的熱點問題之一，是繼全息糾纏熵後在“It from Qubit”框架下考慮的另一個重要概念。理解量子復雜度不僅能夠加深我們對量子信息的理解，結合復雜度幾何框架還能為我們探索時空結構提供新的思路👨🏿‍🎤。Jarzynski恒等式是近年來非平衡態熱力學的重要研究進展。

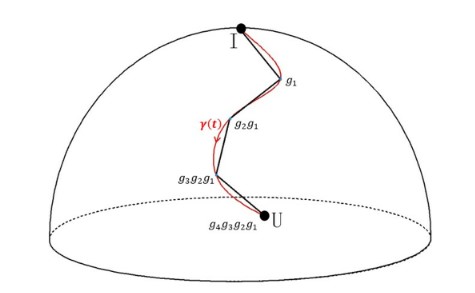
本次發表在《Journal of High Energy Physics》的論文中👨🏻‍🔬，作者通過47頁的篇幅成功地在復雜度幾何的背景下推導出了復雜度版本的Jarzynski恒等式，並類比非平衡態熱力學中的理論框架——軌跡熱力學研究了含時哈密頓量描述的量子系統的復雜度第二定律以及復雜度的漲落-耗散定理👷🏼‍♂️。根據前人對定態哈密頓量描述的量子系統的討論，任何降低復雜度的操作都是不穩定的。

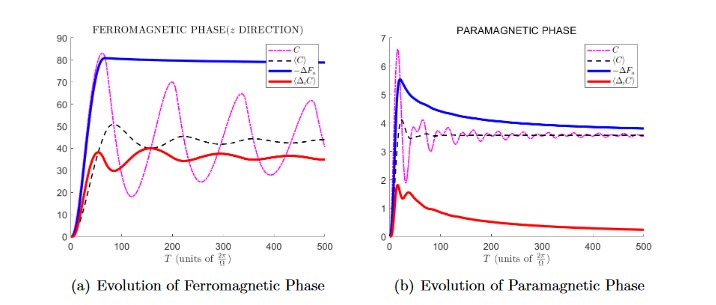
而本文利用軌跡熱力學框架對將該結果推廣到了含時哈密頓量量子系統中👍🏻，結合數值模擬驗證了復雜度第二定律的正確性𓀈，並對復雜度的資源理論進行了討論🍃，這將給研究量子復雜度的性質帶來新的理解🔬。此外，在AdS/CFT框架下，由於局域量子系統的復雜度被認為可以通過復雜度幾何框架與高一維的時空聯系起來。作者利用得到的Jarzynski恒等式在復雜度和高維時空之間建立了聯系🍋‍🟩，這為量化地研究高維時空的漲落結構提供了新的思路✊🏻。論文得到了《Journal of High Energy Physics》的審稿人的充分肯定⚈🛟，審稿人評論到🤹🏽：“In bridging quantum complexity with nonequilibrium thermodynamics, the paper is creative. The bridge may lead to fruitful future work.”

把握大趨勢🙋🏽‍♂️、下好先手棋，這是万事平台理學院依托“五朵金花”之“量子科技”發展戰略，鼓勵本科生參與科研，提升本科生創新能力的新成果。在“量子科技”發展戰略的指導下👱🏼‍♀️，理學院黨政高度重視、堅定不移地推進全程導師製的開展❤️，鼓勵以數理化國際化研究中心為平臺，以學科競賽、學術科研為載體激發本科生學習興趣、培養創新思維，開展交叉研究➾。

本項研究工作得到了國家自然科學基金委項目（No. 11875184）的資助。