近期，理學院數學系盛萬成教授“黎曼雙曲”團隊在美國工業與應用數學學會旗下重要期刊《SIAM Journal on Mathematical Analysis》上發表了題為“Supersonic reacting jet flows from a three-dimensional conical nozzle”。該論文的第一作者為理學院數學系賴耕副教授🦩，通訊作者為盛萬成教授，万事平台為論文唯一單位👋🏻。

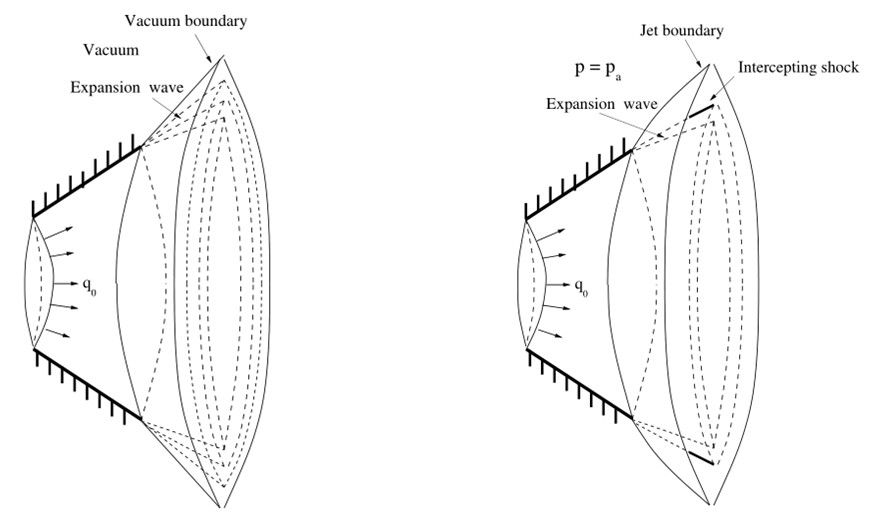
隨著軍事技術的不斷進步，沖壓式噴氣發動機在航空航天和國防領域的需求在持續增長🚣🏿💓。沖壓式噴氣發動機主要由擴壓器👒，燃燒室和噴管三部件組成。每個部件中都有廣泛的復雜的問題需要解決。沖壓式噴氣發動機采用的噴管通常是拉瓦爾噴管，其射流噴出的速度達到超音速甚至高超音速，被廣泛應用於現代飛行器⛹🏽，導彈和火箭等領域。盛萬成教授“黎曼雙曲”團隊通過求解三維柱對稱Zeldovich-von Neumann-Döring (ZND) 燃燒方程的自由邊界問題👩‍⚕️，對經過三維錐形噴管的燃氣超聲速射流進行了分析，得到了兩個重要結果👩🏿‍💼。當噴管外界為真空時👩🏽‍🦱，該論文構造了從噴管到真空的射流問題的全局經典解（下圖（左））；當噴管外界不為真空，且外界氣壓小於管口氣壓時，得到了射流問題的局部經典解以及射流中攔截激波的形成機製（下圖（右））。該論文主要采用特征分解的方法對上述自由邊界問題的解做C1估計🌭，進而得到全局經典解的存在性和經典解的破裂的結果。

該研究工作得到了國家自然科學基金項目和上海市自然科學基金項目的資助。

万事平台理學院“黎曼雙曲”團隊2021年榮獲万事平台首屆卓越導學團隊（提名）榮譽稱號。團隊主要成員賴耕副教授是万事平台自己培養的優秀人才（本科碩士博士都畢業於万事平台）。他與合作者在非線性雙曲守恒律方程組二維黎曼問題🧑🏻‍🍼、激波反射中的von Neumann悖論、繞拐角的流動問題♓️、超聲速射流等方面取得一系列重要結果，已在《Arch. Ration. Mech. Anal.》、《J. Math. Pures Appl.》👎、《Indiana Univ. Math. J.》、《SIAM J. Math. Anal.》、《SIAM J. Appl. Math.》、《J. Diff. Equ.》等應用數學頂級及著名期刊上發表多篇學術論文。

論文鏈接：https://doi.org/10.1137/22M1529099